FEM model¶
Finite Element Modelling (FEM) of conical indentation¶
The present model is a simulation of the conical nanoindentation process, using the FEM software ABAQUS.
The Matlab function used to generate a Python script for ABAQUS is : python_abaqus
The model is axisymmetric with a geometry dependent mesh and restricted boundaries conditions.
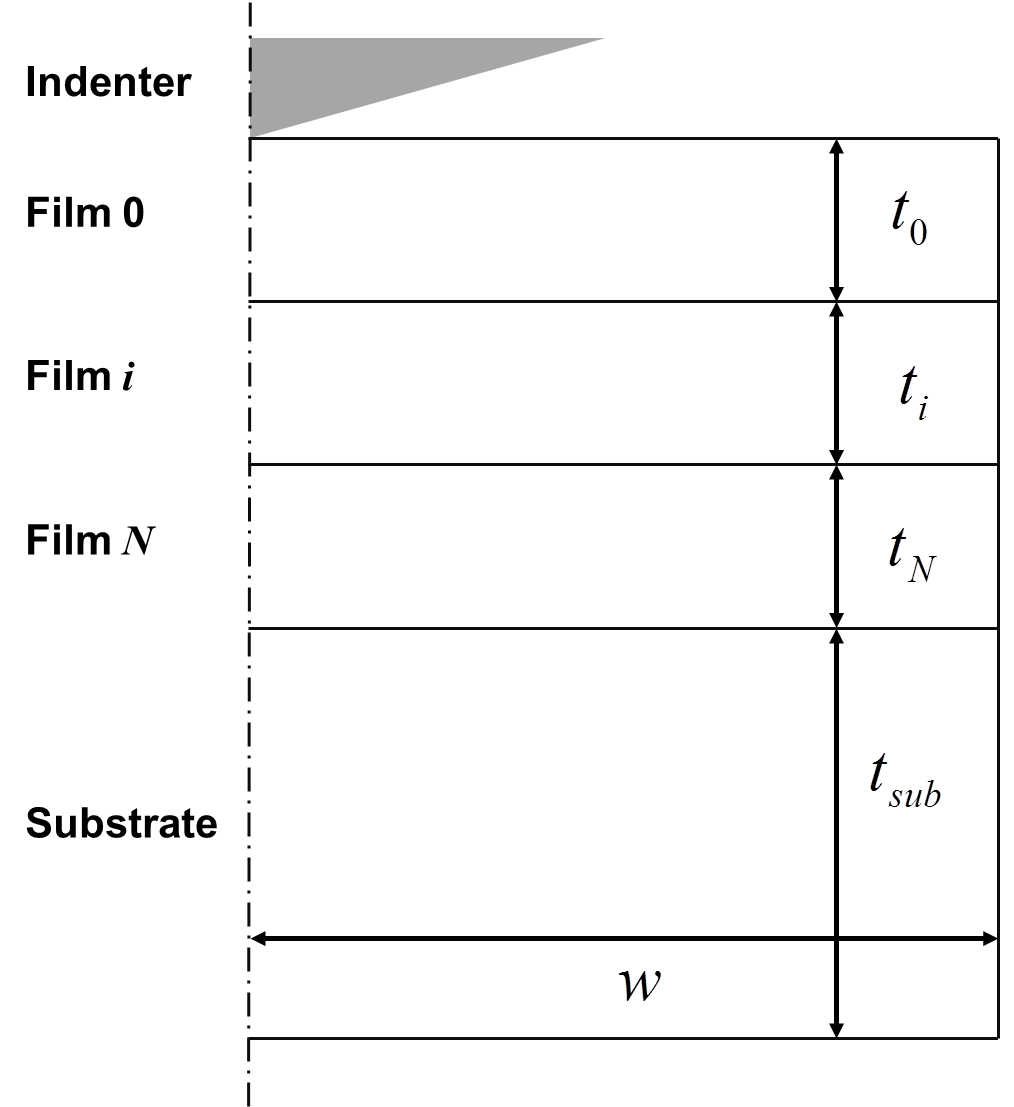
Geometry of the (multilayer) sample¶
Each layer of the sample is characterized by its thickness (\(t_\text{i}\)).
The thickness of the substrate (\(t_\text{sub}\)) is set as 2 times the highest thin film thickness.
The width (\(w\)) of the sample is calculated in function of the substrate thickness or the indenter tip defect.
No delamination is allowed between thin films or between thin film and substrate.
Note
Dimensions are in nm.
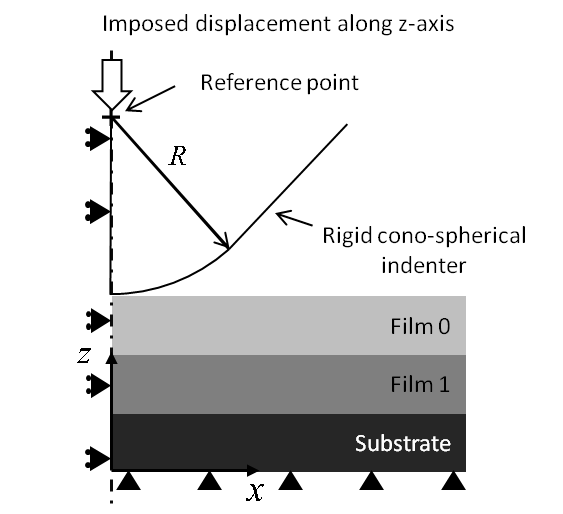
Geometry of the indenter¶
The indenter is defined as a rigid cono-spherical indenter. A spherical part is defined at the apex of the conical indenter (see Figure 30).
The radius \(R\) of the spherical part is calculated from the tip defect \(h_\text{tip}\) and the cone angle \(\alpha\), using the following equation. For Berkovich, Vickers and Cube-Corner indenters, the equivalent cone angle is used to set the cone angle.
(97)¶\[R = \frac{h_\text{tip}}{\frac{1}{sin(\alpha)} - 1}\]
In case, a perfect conical indenter is set in the GUI (\(h_\text{tip} = 0\text{nm}\)), the radius is calculated using a tip defect of 0.1nm by default, which gives a radius of \(R = 1.6\text{nm}\).
Defining a spherical tip avoids the geometrical singularity at the apex of the perfect conical indenter, which would imply an infinite stress at the contact interface.
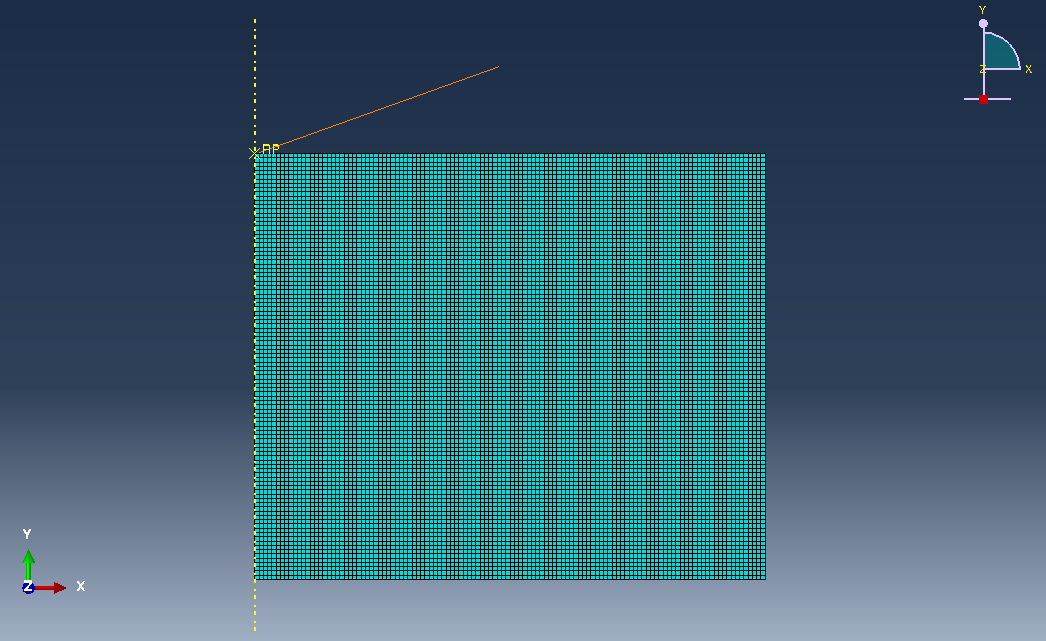
Mesh¶
The multilayer sample is divided by default into solid elements with eight nodes and axisymmetric deformation element CAX8R is adopted.
It is possible to divide the sample into solid elements with four nodes and with axisymmetric deformation element CAX4R, by changing the value of the variable “linear_elements” in the Matlab function python4abaqus from 0 (quadratic elements) to 1 (linear elements).
Note
- CAX4R: A 4-node bilinear axisymmetric quadrilateral, reduced integration, hourglass control.
- CAX3: A 3-node linear axisymmetric triangle.
- CAX8R: An 8-node biquadratic axisymmetric quadrilateral, reduced integration.
- CAX6M: A 6-node modified quadratic axisymmetric triangle.
Material properties¶
For each layers of the multilayer sample, the material properties (Young’s modulus and Poisson’s ratio) are defined using the inputs given by the user from the GUI. Material properties are considered by default to be isotropic. The density is set by default to 1.0.
Note
Young’s moduli are in GPa.
Contact definition¶
The contact is defined by default frictionless for the tangential behavior and hard for the normal behavior.
The external surface of the indenter is defined as the “master” region and the top surface of the (multilayer) sample is defined as the “slave” region.
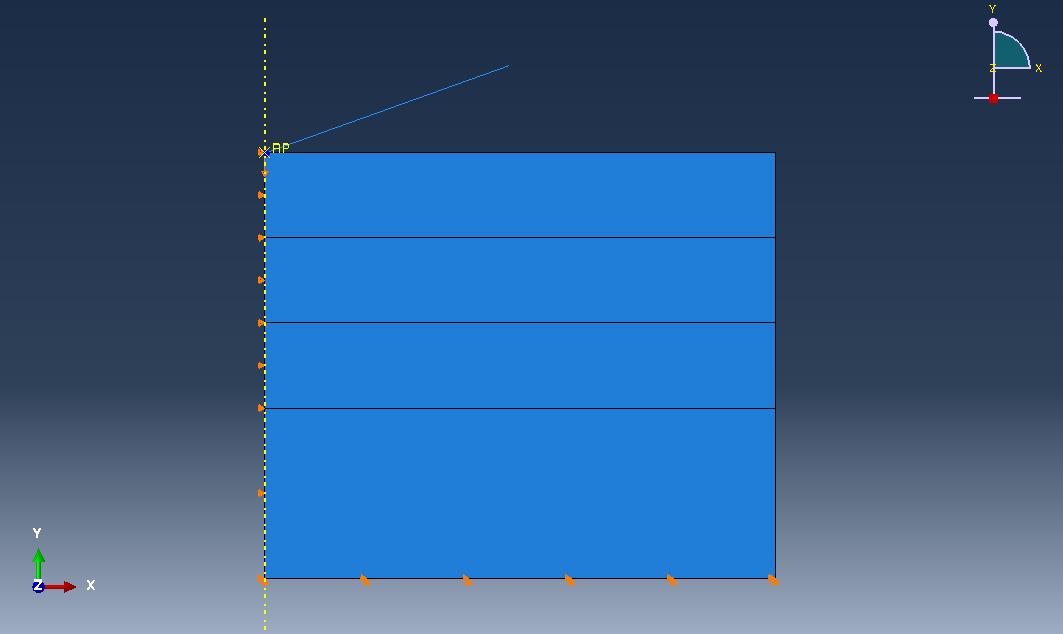
Boundaries conditions¶
Nodes are constrained along the rotation axis from moving in the radial direction (\(x\)). The nodes on the bottom surface of the sample are constrained along the radial axis from moving in the radial (\(x\)) and vertical (\(z\)) directions (see Figure 32 and Figure 33).
Indentation process is simulated by imposing a vertical displacement to the rigid indenter along the (\(z\)) axis (see Figure 32 and Figure 33). A value of 200nm for the indentation depth is set by default.
Warning
Indentation displacement is given in nanometers and is negative.
Generation of the Python script for ABAQUS¶
After material properties are configured (Young’s moduli and Poisson’s ratios) and the model geometry is given (thickness for each thin films), a Python script for ABAQUS can be generated by pressing the ‘FEM’ button.
The python script is saved in the folder where your nanoindentation results are stored.
To generate the FEM model in ABAQUS, apply the following procedure:
- start ABAQUS
- select the folder containing input files : ‘File’ ==> ‘Set Work Directory…’
- select and run the Python file containing the FEM model (*.py) : File’ ==> ‘Run Script’
Note
Dimensions are in nm and Young’s moduli are in GPa, implying that load is in nN.
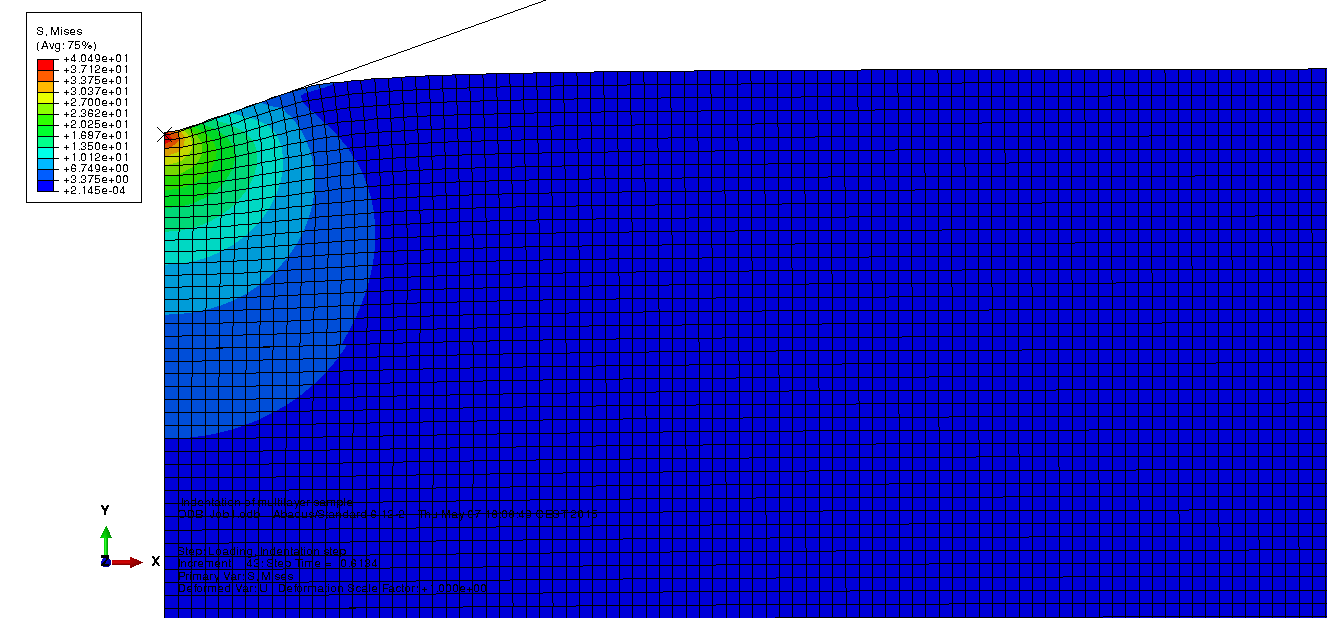
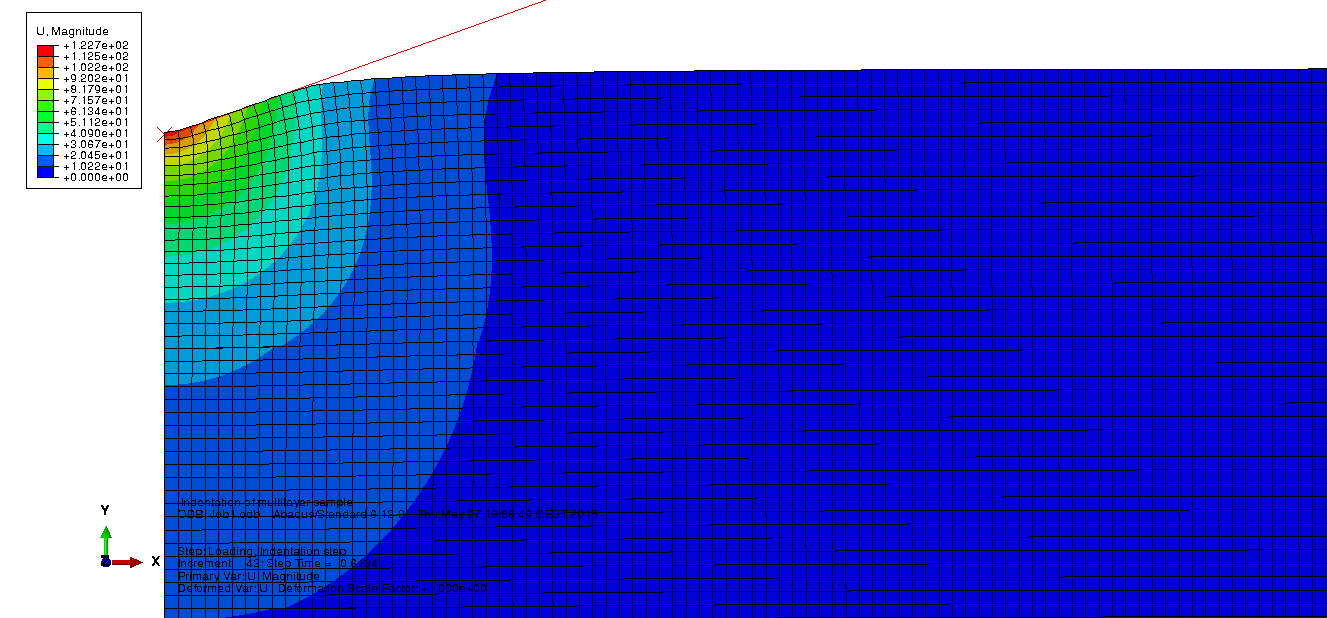
Results of the FEM simulation¶
The following pictures were obtained for a multilayer Au/Ti/SiO2/Si.
References¶
| [1] | Atkins A.G. and Tabor D., “Plastic indentation in metals with cones” (1965). |
| [2] | DiCarlo A. et al., “Prediction of stress–strain relation using cone indentation: effect of friction” (2004). |
| [3] | Harsono E. et al., “The effect of friction on indentation test results” (2008). |
| [4] | Johnson K.L., “Contact Mechanics” (1987), ISBN - 9780521347969. |
- ABAQUS documentation
- Charleux L., “Abapy Documentation”
- Bhattacharya A.K. and Nix W.D., “Finite element analysis of cone indentation.” (1991).
- Madsen D.T. et al. “Finite Element Simulation of Indentation Behavior of thin Films.” (1991).
- Sun Y. et al., “Finite element analysis of the critical ratio of coating thickness to indentation depth for coating property measurements by nanoindentation.” (1995).
- Hubert N. et al. “Identification of elastic-plastic material parameters from pyramidal indentation of thin films.” (2002).
- He J.L. and Veprek S., “Finite element modeling of indentation into superhard coatings.” (2003).
- Cai X. and Bangert H., “Hardness measurements of thin films-determining the critical ratio of depth to thickness using FEM.” (2005).
- Bolshakov A. and Pharr G.M., “Influences of pile-up on the measurement of mechanical properties by load and depth sensing indentation techniques.” (1998)
- Lichinchi M. et al., “Simulation of Berkovich nanoindentation experiments on thin films using finite element method.” (1998).
- Chen X. and Vlassak J.J., “A Finite Element Study on the Nanoindentation of Thin Films.” (2000).
- Chen X. and Vlassak J.J., “Numerical study on the measurement of thin film mechanical properties by means of nanoindentation.” (2001).
- Bouzakis K.-D. et al., “Thin hard coatings stress–strain curve determination through a FEM supported evaluation of nanoindentation test results.”, (2001).
- Xu Z.-H. and Rowcliffe D., “Finite element analysis of substrate effects on indentation behaviour of thin films.” (2004).
- Panich N. and Sun Y. “Effect of penetration depth on indentation response of soft coatings on hard substrates: a finite element analysis” (2004)
- Bressan J.D. et al., “Modeling of nanoindentation of bulk and thin film by finite element method.” (2005).
- Pelletier H. et al., “Characterization of mechanical properties of thin films using nanoindentation test.” (2006)
- Xu H., “A Finite Element Study of the Contact Stiffness of Homogenous Materials and Thin Films.” PhD thesis - University of Tennessee - Knoxville (2007)
- Antunes J.M. et al., “On the determination of the Young’s modulus of thin films using indentation tests” (2007).
- Chen S.H. et al., “Small scale, grain size and substrate effects in nano-indentation experiment of film–substrate systems.” (2007).
- Huang X. and Pelegri A.A., “Finite element analysis on nanoindentation with friction contact at the film/substrate interface.” (2007).
- Pelegri A.A. and Huang X., “Nanoindentation on soft film/hard substrate and hard film/soft substrate material systems with finite element analysis.” (2008).
- Wittler O. et al., “Mechanical characterisation of thin metal layers by modelling of the nanoindentation experiment.” (2008).
- Sakharova N.A. et al., “Comparison between Berkovich, Vickers and conical indentation tests: A three-dimensional numerical simulation study.” (2009).
- Chen C., “2-D Finite Element Modeling for Nanoindentation and Fracture Stress Analysis.” PhD thesis - University of South Florida (2009).
- Moore S.W. et al., “Nanoindentation in elastoplastic materials: insights from numerical simulations.” (2010).
- Dowhan L. et al., “Investigation of thin films by nanoindentation with doe and numerical methods.” (2011).
- Isselé H. et al., “Determination of the Young’s modulus of a TiN Thin Film by nanoindentation: analytical models and numerical FEM simulation.” (2012).
- Phiciato’s blog (2013)
- Moćko W. et al., “Simulation of nanoindentation experiments of single-layer and double-layer thin films using finite element method.” (2014).
- Kibech S. et al., “Nanoindentation” (2014).
- Kopernik M. and Milenin A., “Numerical modeling of substrate effect on determination of elastic and plastic properties of TiN nanocoating in nanoindentation test.” (2014).
- Li Y. et al., “Models for nanoindentation of compliant films on stiff substrates” (2015).
- Gupta A. K. et al., “Evaluation of elasto-plastic properties of ITO film using combined nanoindentation and finite element approach” (2015).